The Halting Problem
Summary
The Halting Problem is a first-order absolute epistemic limit. It says that it is impossible for there to exist a computer program that identifies whether any possible computer program and its input will halt as opposed to run forever. This impossibility is shown through a contradiction that results from running the program on itself. If the program says it halts, then it doesn’t, and if it says it doesn’t halt, then it does. Therefore, such a program can’t exist.
The halting problem demonstrates an absolute limit on an our ability to know the results of certain computational tasks. The only way to know if any possible program will halt is to run it and see. For many algorithms that do not halt during the time we observe them, we will never know if they do or do not halt. To say for sure, we would need to run them for an infinite amount of time, which is time we do not have. Therefore, we have no way of deciding which programs in the space of all possible programs will hault and which will not.
Introduction
Imagine a busy day at your desk job. You have dozens of applications running simultaneously on your computer. Suddenly, it begins to slow down, and one application appears to be stuck in an infinite loop, consuming resources and degrading the performance of the system. Will the application eventually resolve this issue and return to normal? Or will it remain in this state indefinitely? This somewhat mundane, somewhat frustrating scenario illustrates the essence of the halting problem: given a computer program and an input, can we determine if the program will eventually halt or continue running forever? The halting problem demonstrates that the answer is no we can’t.
Explanation
The halting problem asserts that no program can be devised to determine if a program and its input will halt or run forever for all possible pairs of programs and inputs.
We will demonstrate this with a proof by contradiction. The following explanation borrows heavily from Noson Yanofsky’s excellent book, The Outer Limits of Reason. If epistemic limits interest you, I highly recommend it.
The programs we will be examining are everyday computer programs. For example, we could code a program to take a number x and keep adding two to it until the number is greater than or equal to 10, then output the result. Let’s call this program two_adder. So for x = 4, the result would be 10 (4 + 2
Suppose we can construct a program that can determine if any such program and its inputs halt. We’ll call this program halt_decider. We could feed in our program two_adder and a value for x, say 7, and halt_decider will output “two_adder halts” if it halts and “two_adder doesn’t halt” otherwise. Figure 1 below schematically depicts such a program.
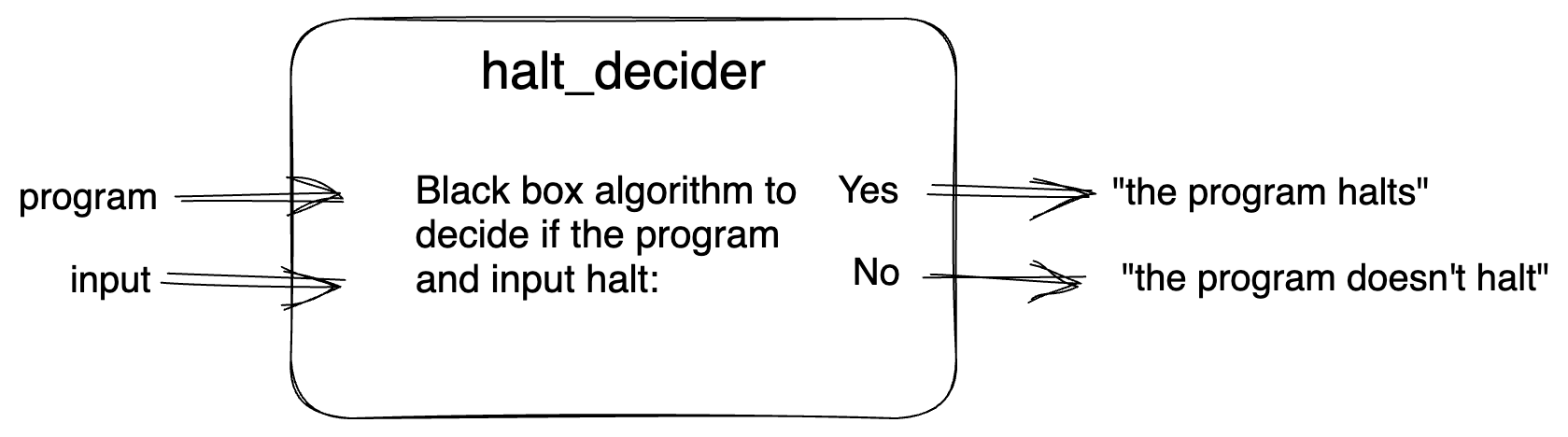
halt_decider program. It takes a program and input and applies an algorithm to decide if the program with the input will halt.Now suppose we can make another program that we’ll call halt_contradictor. It will do something weird. It will take a program and an input value then call halt_decider to see if it halts. If halt_decider indicates the program and input halts, then we’ll have halt_contradictor go into an infinite loop printing “{program name} halts.” If halt_decider indicates that the program does not halt, then halt_contradictor will print one time “{program name} doesn’t halt.” Basically, halt_contradictor takes the output of halt_decider and does the opposite. If the input program halts, halt_contradictor loops forever. If the input program doesn’t halt, halt_contradictor halts. Figure 2 should help clarify this confusing setup.
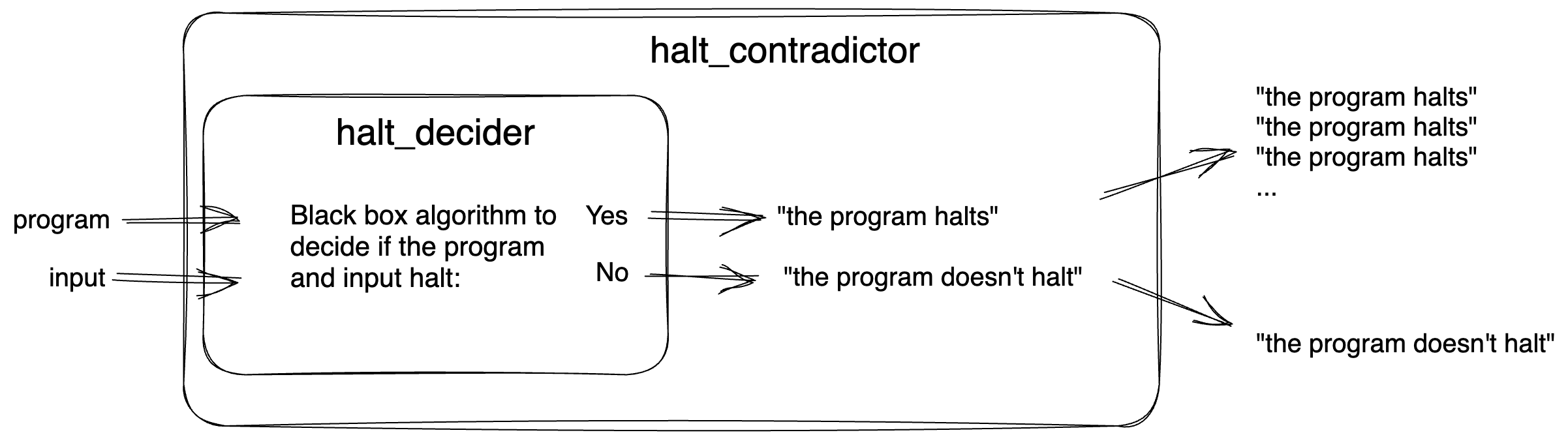
halt_contradictor program. tl;dr: halt_contradictor does the opposite of what halt_decider says. It is built on top of halt_decider and adds the extra step of taking the output of halt_decider and either halts if halt_decider indicates the program doesn’t halt or enters an infinite loop if halt_decider indicates the program halts.Let’s feed in two_adder with an input value of 7 to halt_contradictor. We said earlier it will halt, so halt_decider will indicate “two_adder halts”. Halt_contradictor will take that output and then print “two_adder halts” “two_adder halts” “two_adder halts”….. in an infinite loop.
One final element we need is to number all of our programs. It doesn’t matter how we number them, but each one needs to have a unique reference number. For program two_adder we could assign the number 123, for halt_contradictor we could assign the number 9, etc. Computers have no problem assigning reference keys to represent programs that run in other programs.
Now we will break the program. Since halt_contradictor is a program, let’s feed it into itself! Let’s say that halt_contradictor is the program that is going into halt_contradictor along with the numeric encoding for halt_contradictor that we said was 9. What happens when we do this? If halt_decider says that halt_contradictor halts, it says “halt_contradictor halts.” Halt_contradictor will take that output and do the opposite. It will print “halt_contradictor halts” in an infinite loop. If halt_decider says “halt_contradictor doesn’t halt”, then halt_contradictor will print out “halt_contradictor doesn’t halt” once and then…halt.
Contradiction
Do you see the contradictions?
If
halt_decidersays thathalt_contradictor with thehalt_contradictorprogram and input 9 (numeric encoding of itself) halts, then we saw that thathalt_contradictorwith thehalt_contradictorprogram and input 9 will not halt!Similarly, if
halt_decidersays thathalt_contradictorwith these inputs doesn’t halt, thenhalt_contradictorwith those inputs will halt!
These contradictions arose because we assumed that the halt_decider is a real program. If our assumption leads to a contradiction, then our assumption is false. Therefore, halt_decider cannot exist, and we can conclude there is no program that can solve the halting problem.
Importance
This may seem like a contrived example of self-reference, but its implications are enormous. After the Halting Problem was described, researchers discovered many similar problems. The Halting Problem established the existence of a whole class of problems that are undecidable. Undecidable problems have a clear “yes” or “no” answer, such as “will a program halt?”, but we will never know the answer because no computational method or rational effort can provide the answer. What’s more, if we could solve the Halting Problem, we could solve other undecidable problems such as Goldbach’s Conjecture or compute measures of Kolmogorov complexity, which would representing important advances in the fields of mathematics and probability theory.
Lastly, devastatingly, there are an uncountably infinite number of undecidable problems. There are an uncountably infinite number of questions that no human nor artificial general intelligence can answer. As rational agents navigate the vast landscape of truth, there will forever be a horizon of questions we can ask but have no method of answering. The answers will be out there, beyond us, forever.